Lineare Regelungstechnik¶
graph TD;
A((System));
B[Linear];
C[Nicht Linear];
D[Zeit variant];
E[Zeit invariant];
F[kontinuierlich];
G[diskret];
A-->B;
A-->C;
A-->D;
A-->E;
A-->F;
A-->G;Mehrgrößenregelung¶
Vollständige Modale Synthese¶
Falb Wolovich¶
Riccati Regler¶
Beobachter¶
reduzierter Beobachter¶
Allgemeines (bsp. 3 Tank bild noch einfügen) Für ein SISO Sytem in dem die einzige Messgröße die Temperatur in Tank 3 ist und die einzige stellgröße der Volumenstrom an warmem wasser in Tank 1, gilt:
- Es kann ein vollständiger beobachter entworfen werden, wenn A,C mit dem C das zu der regelgröße am Ausgang führt vollständig beobachtbar ist.
- Ist aufgrund von der DGL z.B. A,C nicht beobachtbar muss man evtl. einen weiteren Zustand hinzunehmen z.B. die Temperatur in Tank 2. Ist mit diesem neuem C dann beobachtbarkeit gegeben so kann ein reduzierter beobachter entworfen werden und alle anderen Zustände z.B. die Temperatur in Tank 1 geschätzt werden.
Blockschaltbild reduzierter beobachter mit Zustandsregler:
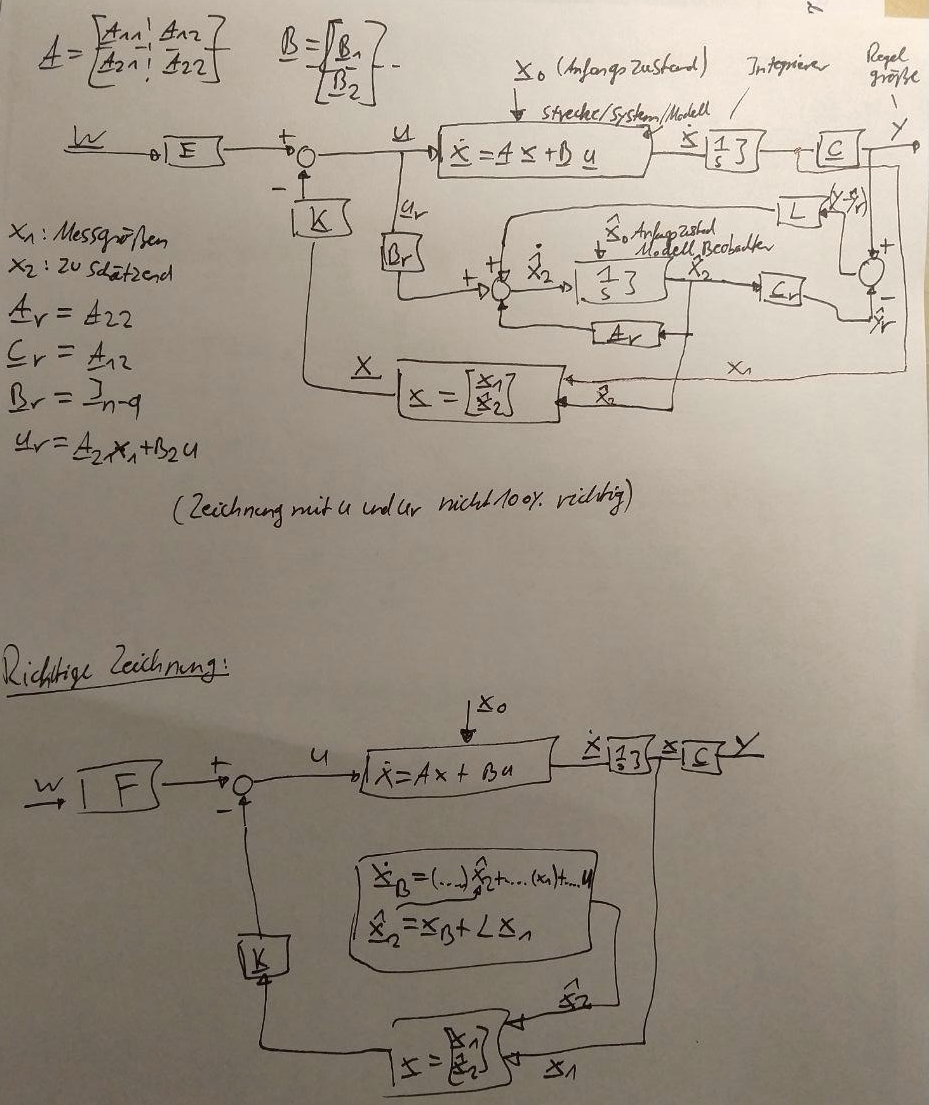
Größen:
-
Nach Transformation auf Sensorkoordinaten ergibt sich:
\[ \begin{equation} \begin{bmatrix}\dot{x}_1 \\ \dot{x}_2 \end{bmatrix} = \begin{bmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix} \cdot \begin{bmatrix}{x}_1 \\ {x}_2 \end{bmatrix} + \begin{bmatrix}{B}_1 \\ {B}_2 \end{bmatrix} u \end{equation} \]dabei beinhaltet \(\mathbf{x}_1\) alle messbaren Zustände und \(\mathbf{x}_2\) alle nicht messbaren Zustände also die Zustände die man beobachten möchte bzw. die Zustände die nicht vorhanden sind und geschätzt werden sollen.
-
Bilde mit reduziertem System das zu beobachtende System:
\[ \begin{equation} \underbrace{\dot{x}_1-A_{11} x_1-B_1 u}_{y_r} = \underbrace{A_{12}}_{C_r} \cdot x_2 \\ \dot{x}_2 = \underbrace{A_{22}}_{A_r}\cdot x_2 +\underbrace{A_{21}x_1+B_2u}_{u_r} \end{equation} \]Dieses System ist dann:
\[ \begin{equation} \dot{x}_2 = A_r x_2+I_{n-q} u_r \\ y_r = C_r x_2 \end{equation} \]q ist die Anzahl der Messgrößen. n die Anzahl aller Zustände.
-
Wende Beobachter für reduziertes zu beobachtendes System {r} an:
\[ \begin{equation} \dot{\hat{x}}_2 = A_r {\hat{x}}_2 + B_r u_r + L(y_r - \hat{y}_r) \\ y_r = \dot{x}_1-A_{11} x_1-B_1 u \\ \hat{y}_r = A_{12} \hat{x}_2 \\ \text{Einsetzen ergibt:} \\ \dot{\hat{x}}_2 = (A_{22}-L A_{12})\hat{x}_2 + A_{21} x_1 + B_2 u + L (\dot{x}_1-A_{11} x_1-B_1 u) \end{equation} \] -
Transformiere System auf (b) (Trick um \(\dot{x}_1\) wegzubekommen)
\[ \begin{equation} {{x}}_b = \hat{x}_2 - L x_1 \quad \text{Transformation!} \\ \dot{{x}}_b = \dot{\hat{x}}_2 - L \dot{x}_1 \\ \dot{{x}}_b = (A_{22}-L A_{12})\hat{x}_2 + A_{21} x_1 + B_2 u + L (\dot{x}_1-A_{11} x_1-B_1 u) - L \dot{x}_1 \\ \dot{{x}}_b = (A_{22}-L A_{12})\hat{x}_2 + A_{21} x_1 + B_2 u + L (-A_{11} x_1-B_1 u) \\ \end{equation} \]In der letzen gleichung hängt das transformierte System nun nicht mehr von einer Ableitung (\(\dot{x}_1\)) ab. Um nun aber am Ende \(\hat{x}_2\) zu berechnen wenden wir:
\[ \begin{equation} \hat{x}_2 = {{x}}_b + L x_1 \quad \text{Transformation!} \end{equation} \] -
Formuliere \(\dot{{x}}_b\) um:
\[ \begin{equation} \hat{x}_2 = {{x}}_b + L x_1 \quad \text{einsetzen in:}\\ \dot{{x}}_b = (A_{22}-L A_{12})\hat{x}_2 + A_{21} x_1 + B_2 u + L (-A_{11} x_1-B_1 u) \\ \dot{x}_b = (A_{22} - LA_{12})x_b + (B_2 - LB_1)u+ (A_{21}+A_{22} L - L A_{12}L-LA_{11})x_1 \\ \end{equation} \] -
Geschlossener Regelkreis mit red. Beobachter
Annahme es existiert ein geschlossener Regelkreis mit dem Regler:
\[ \begin{equation} u = -\begin{bmatrix} K_1 & K_2 \end{bmatrix} \begin{bmatrix} x_1 \\ \hat{x}_2 \end{bmatrix} + F \cdot w \\ u = -\begin{bmatrix} K_1 & K_2 \end{bmatrix} \begin{bmatrix} x_1 \\ {{x}}_b + L x_1 \end{bmatrix} + F \cdot w \end{equation} \]Dann lässt sich dies nun durch einsetzen von u in \(\dot{x}_1\), \(\dot{x}_2\) und \(\dot{x}_b\) schreiben als:
\[ \begin{equation} \begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_b \end{bmatrix} = \begin{bmatrix} A_{11} - B_1 \tilde{F} & A_{12} & -B_1 K_2 \\ A_{21}-B_2 \tilde{F} & A_{22} & -B_2 K_2 \\ \tilde{H} - \tilde{B} \tilde{F} & 0 & A_{22} - L A_{12} - \tilde{B} K_2\end{bmatrix} \cdot \begin{bmatrix} {x}_1 \\ {x}_2 \\ {x}_b \end{bmatrix} + \begin{bmatrix} {B}_1 F \\ {B}_2 F \\ \tilde{B} F \end{bmatrix} \cdot w \end{equation} \]mit Abkürzungen (tilde) :
\[ \tilde{H} = A_{21} - L A_{11} +(A_{22}-L A_{12})L \\ \tilde{B} = B_2 - L B_1 \\ \tilde{F} = (K_1 + K_2L) \\ \]
Mehr dazu auch in Skript TUHH. Alle buchstaben im obigen sind vektoren bzw. Matrizen (sollten also eig. noch fett geschrieben werden).
Störgrößen Beobachter¶
Robuste Regelung (RR)¶
Symbole¶
Grundlagen¶
Abkürzende Schreibweise für Zustandsraumdarstellung:
Sei der Zählergrad einer Übertragungsmatrix n und der Nennergrad m. Dann nennt man die Übertragungsfunktion:
- proper: \(n \leq m\)
- streng proper: \(n<m\)
Untermengen von Übertragungsfunktionen:
- \(\b{G}(s) \in \mathcal{R} \mathcal{H}_2\) Übertragungsmatrix enthält nur stablie streng propere rationale Übertragungsfunktionen
- \(\b{G}(s) \in \mathcal{R} \mathcal{H}_{\infty}\) Übertragungsmatrix enthält nur stablie propere rationale Übertragungsfunktionen
Normierung:
Liegen die Wertebereiche der Ein und Ausgangsgrößen weit auseinander, so unterscheiden sich die Werte in der ZRD oft um viele Größenordnungen. Dies führt einerseits zu numerischen Problemen andererseits lässt sich das System nicht so gut interpretieren. Daher sollte jedes System im ersten Schritt der Modellbildung normiert werden.
Wähle für \(\b{N}_x\) z.B. eine Diagonalmatrix mit typischen oder maximalen Werten. Wenn maximal Werte gewählt, so bietet sich die \(H_{\infty}\) Norm an, denn ist die Norm <1 so beinhaltet dies das Einhalten der maximal Werte.
Push Through Regel:
Verallgemeinerte Strecke:
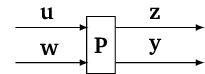
Reglerentwurf im Frequenzbereich¶
Robuste Regelung¶
graph TD;
A-->B;
A-->C;
A-->D;graph LR;
A(node text);
C(( +));
A-->|u|B;
B-->C;
A-->D;
D-->C;digraph finite_state_machine {
rankdir=LR;
size="8,5"
node [shape = doublecircle]; S;
node [shape = point ]; qi
node [shape = circle];
qi -> S;
S -> q1 [ label = "a" ];
S -> S [ label = "a" ];
q1 -> S [ label = "a" ];
q1 -> q2 [ label = "ddb" ];
q2 -> q1 [ label = "b" ];
q2 -> q2 [ label = "b" ];
}
Literatur zu RR¶
Modellbildung¶
Dieses Kapitel bietet eine kurze Zusammenfassung der Modellierung mechanischer & elektrischer Systeme.
Potentialvariable und Flussvariable¶
Mit der Potentialvariale\(e_i(t)\)und der Flussvariable\(f_i(t)\)gilt für die verallgemeinterte Leistung:
Für ein System gilt generell:\(\sum_{i=1}^n P_i(t) = 0\)
Reihen und Parallelschaltung¶
| Schaltungsart | Gesetze | Wiederstand | Kapazität | Induktivität |
|---|---|---|---|---|
| Reihen- schaltung |
\(f_1=f_2=...=f_n\) \(\sum e_i =0 \quad (8)\) mit (8) Maschengleichung für elektrisches Beispiel rechts gilt: \(f=f_1=f_2 \rightarrow I=I_1=I_2\) \(e=e_1+e_2 \rightarrow U=U_1+U_2\) ableiten:\(\dot{I}=Q\) \(\rightarrow Q=Q_1=Q_2\) |
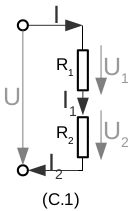 \(U=I\cdot (R_1+R_2)\) \(R_{ges}=R_1+R_2\) |
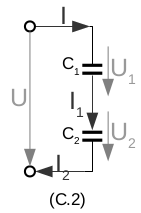 \(Q=C\cdot U\) \(U=\frac{Q_{ges}}{C_{ges}}=\frac{Q_1}{C_1}+\frac{Q_2}{C_2}\) \(\frac{1}{C_{ges}}=\frac{1}{C_1}+\frac{1}{C_2}\) \(C_{ges}=\frac{C_1\cdot C_2}{C_1+C_2}\) |
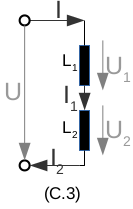 \(L_{ges} = L_1+L_2\) |
| Parallel- schaltung |
\(e_1=e_2=...=e_n\) \(\sum f_i =0 \quad (9)\) mit (9) Knotengleichung für elektrisches Beispiel rechts gilt: \(f=f_1+f_2 \rightarrow I=I_1+I_2\) \(e=e_1=e_2 \rightarrow U=U_1=U_2\) |
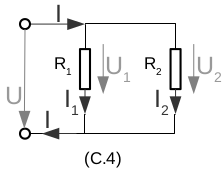 \(R_{ges}=\frac{R_1 \cdot R_2}{R_1+R_2}\) |
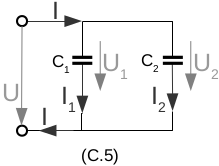 \(C_{ges}=C_1+C_2\) |
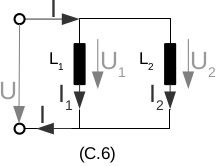 \(L_{ges}=\frac{L_1 \cdot L_2}{L_1+L_2}\) |
Für den elektrischen Fall bedeutet:
- (8) Die Summe aller Spannungen in einem Kreis ist 0.
- (9) Die Summe aller Zufließenden Ströme eines Knotens ist gleich der Summe aller abfließenden Ströme eines Knotens.
Hierbei ist im elektrischen Fall die Potentialvariable e(t) gleich der Spannung U und die Flussvariable f(t) gleich dem Strom I. Für mechanische bzw. hydraulische etc. Systeme kann ebenfalls eine Potentialvariable und Flussvariable festgelegt werden(siehe nachfolgende Tabelle). Zudem kann beispielswiese für den mechanischen Fall auch ein verallgemeinerter Wiederstand, Kapazität und Induktivität angegeben werden. Hiermit lassen sich mechanische Systeme mit der verallgemeinerten Netzwerkanalyse in Systeme mit "elektrischen Bauelmenten: R, L, C, Stromquelle, Spannungsquelle" überführen und anschließend mit den Konten und Maschengesetzen der Elektrotechnik analysieren.
Numerisches Lösen von DGL's¶
Übersichtstabelle Einschrittverfahren¶
| Verfahren | Vorschrift | p | K? | B-T | R(z) | Sta. | S(z) |
|---|---|---|---|---|---|---|---|
| Euler_e | \(y_{n+1} = y_{n} + h \cdot f (t_n, y_n)\) | 1 | ja | \(\begin{array}{cc} {1} & {0} \\ \hline & {1} \end{array}\) | \(z-1\) | 0 | --- |
| Euler_i | \(y_{n+1} = y_{n} + h \cdot f (t_{n+1}, y_{n+1})\) | 1 | ja | \(\begin{array}{cc} {1} & {1} \\ \hline & {1} \end{array}\) | \(\frac{1}{1-z}\) | 0,A,L | --- |
| Heun2_e | \(y_{n+1} = y_{n} + \frac{1}{2} (k_1+k_2)\) \(k_1 =f(t_n,y_n)\) \(k_2=f(t_n+h,y_n+k_1)\) |
2 | ja | \(\begin{array}{cc} {0} \\ 1 & {1} \\ \hline & {1/2} & 1/2 \end{array}\) | \(\frac{1}{1-z}\) | 0 | --- |
| Trapez_i | \(y_{n+1} = y_{n} + \frac{1}{2} (k_1+k_2)\) \(k_1 =f(t_n,y_n)\) \(k_2=f(t_n+h,y_n+1/2 k_1+1/2 k_2)\) |
2 | ja | \(\begin{array}{ccc} {0} \\ 1 & {1/2} & 1/2 \\ \hline & {1/2} & 1/2 \end{array}\) | \(\frac{1}{1-z}\) | 0,A | -dd-- |
| Mittelp._i | \(y_{n+1} = y_{n} + f(t_n+\frac{1}{2}h, \frac{1}{2} y_{n+1})\) | 2 | ja | \(\begin{array}{cc} {1/2} & 1/2 \\ \hline & 1\end{array}\) | \(\frac{1}{1-z}\) | 0 | 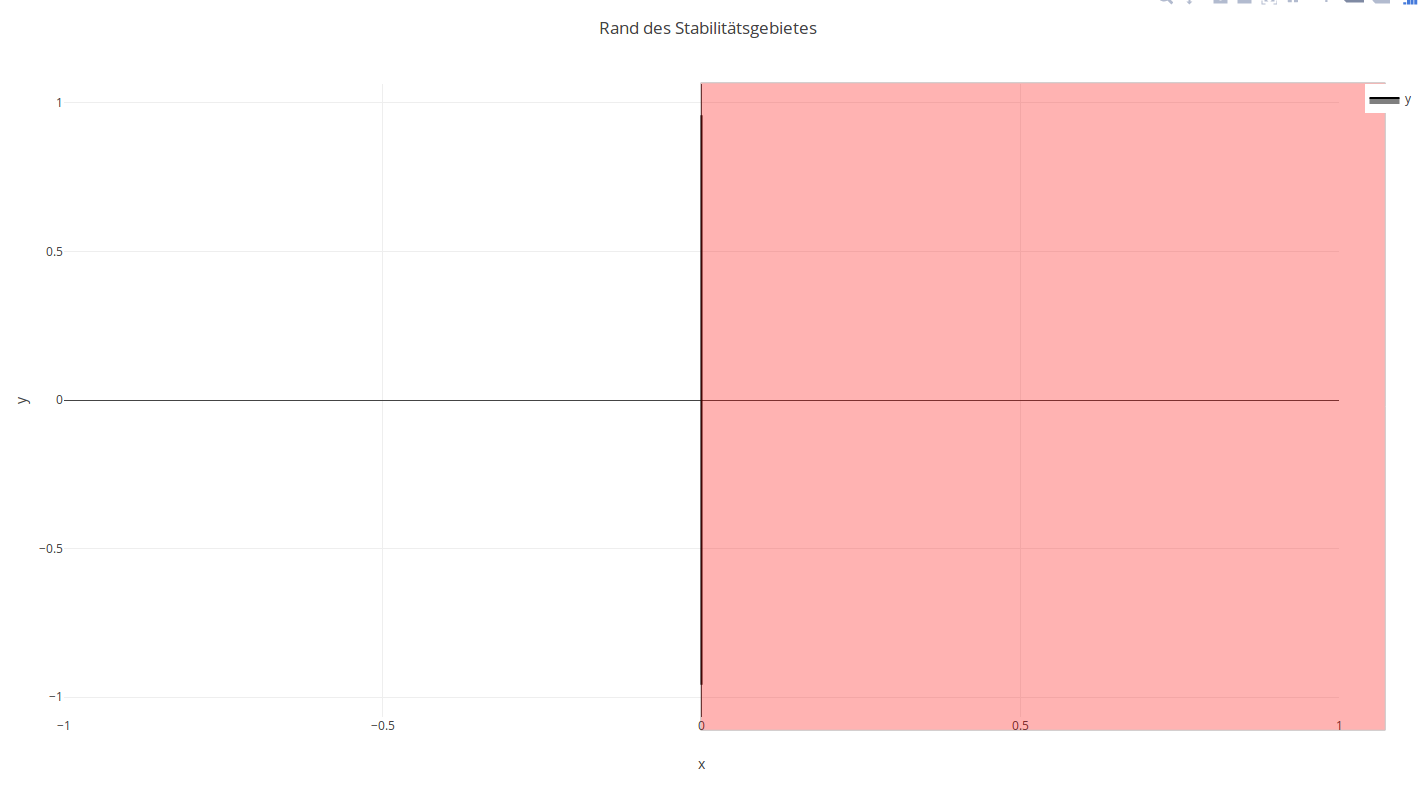 |
| RK2_e | \(y_{n+1} = y_{n} +(k_2)\) \(k_1 =f(t_n,y_n)\) \(k_2=f(t_n+\frac{1}{2}h, y_n+\frac{1}{2}k_1)\) |
2 | ja | \(\begin{array}{cc} {0} \\ 1/2 & 1/2 \\ \hline & {0} & 1 \end{array}\) | \(\frac{1}{1-z}\) | 0 | --- |
| Simpson_e =RK3_e |
für explizite-RK gilt allgemein: \(\Phi=\sum_{j=1}^{s} b_j k_j, \quad k_1=f(t,y)\) \(k_j=f(t+c_j h, y+h\sum_{l=1}^{j=1}a_{jk}k_l\) s: Stufenzahl, j=2...s, \(y_{n+1}=y_n+h\Phi\) |
3 | ja | \(\begin{array}{ccc} {0} \\ 1/2 & {1/2} \\1&-1&2 \\ \hline & {1/6} & 4/6 & 1/6 \end{array}\) | \(\frac{1}{1-z}\) | 0 | --- |
| Heun3_e | allgemeine Konsistenz Ordnungsregeln: Voraussetzung: \(\sum a_{ij} = c_i\) inv. gegen Autonomisierung p=1: \(\sum b_i = 1\) p=2: \(\sum b_i c_i = \frac{1}{2}\) p=3: \(\sum b_i c_i^2=\frac{1}{2}, \quad \sum b_i a_{ij} c_j = \frac{1}{6}\) |
3 | ja | \(\begin{array}{ccc} {0} \\ 1/3 & {1/3} \\2/3&0&2/3 \\ \hline & {1/4} & 2/4 & 1/4 \end{array}\) | \(\frac{1}{1-z}\) | 0 | --- |
| RK4_e | \(y_{n+1} = y_{n} + \frac{1}{6} \cdot (k_1+2k_2+2k_3+k_4)\) \(k_1 =f(t_n,y_n)\) \(k_2=f(t_n+\frac{h}{2},y_n+\frac{h}{2}\cdot k_1)\) \(k_3=(t_n+\frac{h}{2},y_n+\frac{h}{2}\cdot k_2)\) \(k_4=f(t_n+h,y_n+h \cdot k_3)\) |
4 | ja | \(\begin{array}{ccccc} 0\\ \frac{1}{2} & \frac{1}{2}\\\frac{1}{2} &0 &\frac{1}{2} \\1& 0& 0& 1\\\hline & \frac{1}{6} &\frac{1}{3} &\frac{1}{3} &\frac{1}{6} \end{array}\) | \(\frac{1}{1-z}\) | 0 | --- |
| RKM_e3 | mit p=4 bzw. 5 |
Dabei ist:
- Euler_e --> Explizites Euler Verfahren (i=implizit)
- h die Schrittweite,
- R(z) die Stabilitätsfunktion mit \(z=\lambda \cdot h\):
- S(z) das Stabilitätsgebiet (dargestellt in weiß),
- p=Konsistenzordnung,
- K?: Konvergent? --> für Einschrittverfahren(ESV) gilt Konsistenzordnung = Konvergenzordnung, Konsistenz+0-Stabilität=Konvergenz
- B-T: Butcher Tabelau mit:\(\begin{array}{c|c} \mathbf{c} & \mathbf{A} \\ \hline & \mathbf{b} \end{array}\)
- Sta. = Stabilität z.B. 0-(Dahlquist-stabil), \(\alpha\) Winkelgebiet in linker Ebene (kein ESV ist \(\alpha\) stabil), A-Stabil(komplette linke Ebene), L(Limes Stabil) --> wenn A-stabil und \(\lim\limits_{Re(z) \rightarrow -\infty}{R(z)} = 0\)
Für obige Tabelle können die Butcher Tableaus hier2 überprüft werden.
Daneben gibt es noch weitere Verfahrens Konstruktions-Möglichkeiten:
- adjungierte Verfahren z.B. erst anwenden des Impliziten Euler(IE) Verfahrens und anschließend das Explizite Euler(EE) Verfahren hierdurch entsteht die Mittelpunktsregel bzw. die implizite Trapezregel wenn man erst das IE und dann das EE Verfahren anwendet. Hieraus entstehen dann oft selbstadjungierte Verfahren, die die günstige Eigenschaft haben, dass man pro Schritt 2 Ordnungen gewinnt? (TODO: passt das so?)
- Extrapolation: Gehe erst einen Schritt mit Schrittweite h und anschließend mit Schrittweite h/2 des gleichen Verfahrens und extrapoliere anschließend: So erhält man eingebettete Verfahren.
Übersichtstabelle Mehrschrittverfahren¶
| Verfahren | Vorschrift | p | K? | B-T | R(z) | Sta. | S(z) |
|---|---|---|---|---|---|---|---|
| BDF1_i | --- | --- | --- | --- | --- | --- | --- |
| BDF2_i | --- | --- | --- | --- | --- | --- | --- |
| PEC_e | --- | --- | --- | --- | --- | --- | --- |
| MPEC_e | --- | --- | --- | --- | --- | --- | --- |
Dabei ist:
- BDFp = Backward Formulation Difference
- PEC=Predictor Evaluation Correction
- MPEC:= Modifiziertes PEC
Schrittweitenwahl¶
Möchte man ein System von ODE's (also eine ZRD) mittels eines ESV oder MSV simulieren, so muss man die Schrittweite so wählen, dass man immer im Stabilitätsgebiet ist. Hierbei muss Eigenwert*h innerhalb von S liegen.
Simulation von linearen Systemen¶
Möchte man für ein lineares Zustandsraum-System der Form:
die einzelnen Zustandsgrößen \(\mathbf{x}(t)\) zu jedem Zeitpunkt berechnen, so gibt es grundsätzlich zwei Möglichkeiten:
- Das Aufteilen der DGL in eine homogene und partikuläre Lösung siehe hier
- Das einbinden der Stellgröße u in eine homogene DGL der Form\({\dot{\tilde{\mathbf{x}}}} = \mathbf{\tilde{A}} \mathbf{\tilde{x}}\)und das anschließende Lösen dieser homogenen DGL (dieses Verfahren nennt man Eingangsgrößen-Modellierung).
Zu beachten ist hierbei, dass beide Verfahren exakte Lösungen berechnen. Möchte man hingegen nichtlineare DGL-Systeme analysieren ist die exakte Lösung in der Regel nicht bekannt und man ist auf numerische Näherungsverfahren wie zum Beispiel den Runge-Kutter-Verfahren angewiesen.
Aufteilen in homogene und partikuläre Lösung¶
Die geschlossene Lösungsformel lässt sich mittels der Transitionsmatrix\(\mathbf{\Phi}(t) = e^{\mathbf{A}t}\)berechnen:
Diskretisiert man nun die obige Gleichung mit:
*\(t_0 = t_k\) *\(t = t_{k+1}\) *\(t-t_0 = T\)
Annahme\(\mathbf{u}(t)\)ist eine Treppenfkuntion auf\([t_k, t_{k+1})\)mit konstantem Wert\(\mathbf{u}_k\)
Nun folgt mit der Substitution\(t_{k+1} - \tau = v\):
Mit:
- homogener Lösung:\(\mathbf{\Phi}(T) \mathbf{x}(t_k)\)
- partikulärer Lösung:\(\int_{0}^T \mathbf{\Phi}(v) \mathbf{B} dv \cdot \mathbf{u}_k\)
- und der Koeffizientenmatrix:\(\mathbf{H}(t) = \int_{0}^T \mathbf{\Phi}(v) \mathbf{B} dv\)
Zu beachten ist hierbei, dass nur wenn\(\mathbf{u}(t)\)eine Treppenfkuntion ist, die Zustände mit obiger Formel exakt berechnet werden können. Hierfür ist die zunächst die Berechnung der Transitionsmatrix und anschließend die Berechnung der Koeffizientenmatrix nötig.
Diese Herleitung wurde [0] S.104 entnommen.
Berechnen der Transitionsmatrix¶
Es gibt mehrere Möglichkeiten die Transitionsmatrix zu berechnen:
- A liegt in Diagonalform vor:\(e^{A*t}= \begin{bmatrix} e^{a_{11}t} &0 \\ 0&e^{a_{22}t}\\ \end{bmatrix}\)
- A nicht diagonal aber alle EW von A einfach:\(\Phi (t)=Te^{T^{-1}AT}T^{-1}, \quad T=[ev1, ev2, ...]\)
- Wenn A mehrfache EW enthält unterscheide ob komplex oder doppelt und wende Satz von Leonard an.
- direkt mittels der inversen Laplace Transformation
- über den Reihenentwicklungsansatz
- mit dem Verfahren von Plant (numerisch)
- mit dem modifizierten Verfahren von Plant (numerisch)
Berechnen der Koeffizientenmatrix¶
TODO
Eingangsgrößen Modellierung¶
TODO
Literatur¶
- [0] Prof. Dr.-Ing U. Konigorski: Modellbildung und Simulation - Skrtiptum der TU - Darmstadt
- [1] Antoulas Athanasios C.: Approximation of Large-Scale Dynamical Systems. Philadelphia: siam, 2005.
- [2] Föllinger, O.: Regelungstechnik: Einführung in die Methoden und ihre Anwendung. 11. Auflage, Berlien, Offenbach: VDE Verlag 2013.
- [0] http://me-lrt.de/v1-6-mehrschrittverfahren
Fußnoten¶
-
Lorem ipsum dolor sit amet, consectetur adipiscing elit. ↩
-
check here for BT: https://de.wikipedia.org/wiki/Runge-Kutta-Verfahren ↩
-
Das Runge-Kutta-Merson(KRM_e) Verfahren ist dabei ein Verfahren das zur Schrittweitensteuerung eingesetzt wird. Mehr dazu gibt es hier: https://www.encyclopediaofmath.org/index.php/Kutta-Merson_method ↩